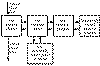
[Turku PET Centre] [PET data analysis] [Main page] [Previous page] [Next page]
All available qualitative information of physiology and biochemistry of tracer is collected to provide a basis for interpretation of tracer kinetic measurements.
Basic steps to describe the transport of tracer from blood to tissue are:
Comprehensive model of labeled receptor binding ligands in brain tissue. This model is far too complicated to be used to analyze PET studies.
In PET studies the tracers are introduced into the body by intravenous injection or inhalation. Tracers are well mixed in the blood in heart chambers, so all arterial blood has the same concentration. Therefore, the concentration of the tracer (model input) delivered to the tissue capillaries can be obtained from any peripheral artery, and the amount of tracer delivered to tissue is proportional to the blood flow (perfusion).
Fraction of the tracer is extracted into tissue across the capillary wall, while the unextracted fraction is washed away by the venous blood flow.
Compartmental model for tracer delivery and extraction to tissue [Graham 1985].
According to this compartmental model, the unidirectional extraction fraction E is related to blood flow F and the capillary permeability-surface product of the tracer PS with equation E=PS/(PS+F). Because of the back transport from tissue to blood, the net extraction fraction (arterivenous concentration difference divided by the arterial concentration) is usually lower than unidirectional extraction fraction.
Modeller must know the mechanism of tracer transport across the capillary wall. Active transport (requires energy) can have a net flux of substance moved against a concentration gradient, while in passive transport the direction of net flux is determined solely by the direction of the concentration gradient across the membrane. Passive transport can be subdivided into facilitated transport and passive diffusion. When the concentration gradient of the molecule is kept steady by constantly supplying and depleting molecules at opposite sides of membrane, the net flux in passive diffusion is related only to the diffusion coefficient and the gradient. In some tissues substances can also cross the capillary wall by bulk flow through openings between the capillary endothelial cells. Facilitated transport, by special carriers in the membrane, allows a selective and regulated uptake of many important substrates, such as glucose and amino acids.
Facilitated transport can be considered as consisting of three steps: the combination of the substrate molecule with the carrier molecule, the assisted movement of the substrate-carrier complex, and the release of the substrate on the other side of the membrane. This process is very similar to the enzyme catalyzed chemical reaction, being saturable and affected by competitive inhibition, and can usually be characterized with similar terms by its maximal transport rate (Vmax) and half-saturation concentration (KM). For natural substrate S, the facilitated transport is not a linear process, but for labeled tracer, which has a low concentration, the linearity holds, and transport process is describable by compartmental models. Permeability-surface product PS can be expressed in terms of Michaelis-Menten constants and the concentration of natural substrate [S] as PS=Vmax/(KM+[S]).
Most chemical reactions in living tissues are catalyzed by enzymes, and can be described with Michaelis-Menten kinetics. For the tracer, the equation is linear with respect to its concentration; linearity holds even when the reactions are not following strictly Michaelis-Menten kinetics, as far as the concentration of tracer is low as compared to the natural substance.
A comprehensive model for labeled neuroreceptor-binding ligand. After the ligand is extracted from the vascular space, it binds to nonspecific binding sites in the interstitial and the cellular spaces. Some ligand molecules diffuse to the synapses of neural cells and bind to the specific neuroreceptors. The bindings to both specific and nonspecific binding sites are reversible.
Garfinkel D. Computer modeling, complex biological systems, and their simplifications. Am J Physiol 1980; 239: R1-R6.
Khoshmanesh K, Kouzani AZ, Nahavandi S, Baratchi S, Kanwar JR. At a glance: cellular biology for engineers. Comput Biol Chem 2008; 32: 315-331.
Phair RD. Development of kinetic models in the nonlinear world of molecular cell biology. Metabolism 1997; 46:1489-1495.