Model validation
Almagest
Kinetic validation
Kinetic validation is done to find out whether the model is quantitatively consistent with the experimental tracer kinetic data. Inconsistent models are rejected; usually, the kinetic and biochemical information gained in the validation studies is useful for reformulating the model. Mismatches are revealed by the existence of nonrandom residuals; the difference between the experimental data and the response function fitted to the data has some time-dependent pattern [Motulsky and Ransnas 1987].
The standard errors of the estimates also needs to be considered to determine the reliability of the estimated parameters. Large standard errors of the estimates usually mean that the data are very noisy or that the number of variable parameters in the model is more than necessary (overparameterization). Statistical methods (Schwartz criterion, Akaike Criterion, F test; see Landaw and DiStefano 1984 or Giatting et al. 2007 ) that consider the goodness of fit versus the number of parameters in the model should be used to guide the selection among alternative models. The noise level in the data affects the number of parameters that may be estimated from the data and usually is the primary determinant of the precision in the estimated parameters. To determine the range of optimized parameter values, Monte Carlo simulations are recommended. The alternative approach, using covariance matrices, requires the assumption that the process being modelled is linear. Since most of the kinetic models of metabolism are nonlinear, this assumption is invalid [Graham 1985].
The choice of the model should not be done solely according to identifiability criteria (e.g. F test). A non-identifiable model may permit the determination of the range of some meaningful parameters, while with an identifiable model one may compute the exact value of some parameters deprived of any physical or physiological meaning.
If the correlation between two estimated parameters is very high, then the likelihood of determining a unique set of values for the parameters is low [Budinger et al. 1985]; this suggests that either of the parameters should be fixed or the model should be reduced.
Biochemical validation
A critical test of the validity of a model is to compare the biochemical results predicted from the kinetic data by the model with those measured directly by chemical means (e.g. microdialysis or biopsy samples). These studies not only provide the time course of total radioactivity in plasma and in the target organ, but also differentiate between the original tracer and its metabolites.
Intervention studies can be performed to estimate the sensitivity of the kinetic data and estimates to the physiologic parameter of interest. Model parameters of interest should change in the proper direction and by an appropriate magnitude in response to a variety of biologic stimuli. In addition, it is useful to test whether the parameters of interest do not change in response to a perturbation in a different factor, e.g. does an estimate of receptor density remain unchanged when blood flow is increased [Carson 1991].
The assumptions made in the reduction of model should be tested, either by explicit experimentation or at least by computer simulation. Simulations provide the magnitude of bias in the parameter estimates due to errors in various assumptions.
The absolute accuracy of model parameters should be tested with a "gold standard", if one is available for the measurement of interest (e.g., the microsphere technique for blood flow measurements). It should be noted that e.g. scanner resolution and change in the physical meaning of parameters due to model reduction can make the comparison of results difficult.
The validation of a PET method for a neuroreceptor assay can be done by comparing the results with those obtained from in vitro binding experiments. However, caution must be exercised in these comparisons. Binding discrepansies between in vitro and in vivo conditions have been observed. In in vitro receptor binding experiments, the concentration of the unbound ligand is uniform, while the uniformity of the unbound ligand concentration in tissue in vivo is less likely to be maintained owing to a multiplicity of factors such as the fast binding-rebinding phenomenon in the synaptic zone and diffusional restrictions. In addition, the ligand binding characteristics of receptor systems have been shown to have large species-to-species differences in both KD and Bmax values [Huang et al. 1986].
Test/retest studies
Test/retest studies provide an estimate of the within-subject variability (lack of reproducibility) of the method. However, reproducibility is only one aspect of the problem. A simple ratio provides more reproducible results than a model based method. Yet, the model based method might reveal true between-subject or treatment differences that are ignored or "normalized" by empirical methods.
Repeatability is estimated by calculating the mean and standard deviation of the absolute values of the difference between test and retest values. Repeatability coefficient (RC) is recommended by the British Standards Institution (1976), and when applied to PET test-retest studies, it is defined as RC = 2 * SD(scan1 - scan2). Assuming that the data is normally distributed, in 95% of the cases the difference between the two measurements will be less than the repeatability coefficient (Bland and Altman, 1986). To facilitate comparisons across regions of interest, test-retest variability (TRV) can be calculated as the absolute value of the difference between test and retest values, divided by the mean of both measurements [Parsey et al. 2000]. The mean TRV percentage ± SD should be reported.
The intraclass correlation coefficient (ICC) (Shrout and Fleiss, 1979) is a useful measure of reliability, as this statistical parameter compares the within-subject (WS) variability to the between-subject (BS) variability in repeated observations.
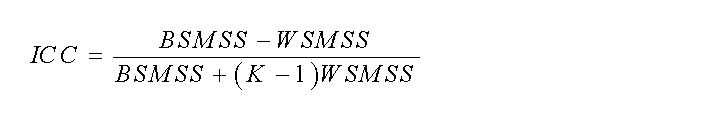
In the one-way ANOVA model, BSMSS is the mean sum of squares between subjects, WSMSS is the mean sum of squares within subjects, K is the number of repeated observations (K=2 in test-retest study) and N is the number of subjects.
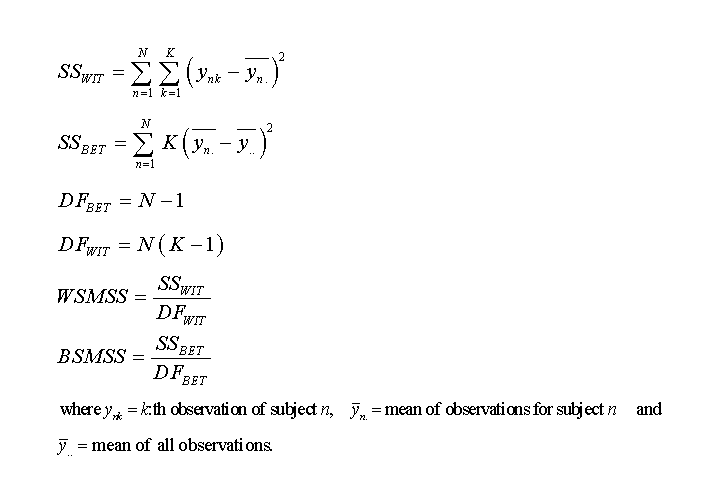
Negative ICC value indicates that more differences are observed within than between subjects. ICC ranges between -1 (no reliability, i.e. BSMSS=0) to 1 (maximum reliability, achieved in the case of identity between test and retest, i.e. WSMSS=0) [Parsey et al. 2000]. As a rule, the method with the highest reliability (higher ICC) should be chosen [Laruelle 1999].

