[18F]FDG
[18F]FDG model
The autoradiographic method for measuring regional metabolic rate of glucose in the brain of rat using [14C]deoxyglucose (Sokoloff et al. 1977) has been modified for human studies using positron emission tomography (PET) and [18F]2-fluoro-2-deoxy-D-glucose ([18F]FDG) by Phelps et al. (1979) and Reivich et al. (1979).
The three-compartment model with four rate constants K1*, k2*,
k3* and k4* is often simplified by assuming that the
dephosphorylation rate of FDG-6-phosphate in brain tissue is small enough that
it can be ignored (k4*=0).
At least a part of the observed k4* may be explained by tissue
heterogeneity (Schmidt et al., 1992).
Metabolic rate of glucose (MRglu) can be calculated from equation
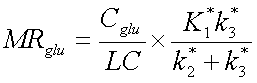
, where Cglu is the concentration of glucose in plasma and LC
is the lumped constant.
Originally FDG studies were always analyzed using compartment model with the three or four rate constants. Only later it was found out that a graphical method, s.c. Gjedde-Patlak plot (Patlak and Blasberg, 1985) can be used to directly estimate the combination of the model rate constants. This combined term, uptake rate for FDG (Ki*=K1*k3*/(k2*+k3*)) is robust and very fast to calculate, and is therefore also suitable for computation of parametric images.
Lumped constant (LC)
The lumped constant of Sokoloff et al. (1977) is based on the biochemical principles of competitive substrate kinetics. It accounts for the differences in transport and phosphorylation rates between D-glucose and 2-fluoro-2-deoxy-D-glucose, and is used to transform the FDG uptake rate to glucose uptake rate.
A common assumption in brain FDG studies is that lumped constant is uniform over the whole brain and in all subject and patient groups. Hexokinase favours glucose over FDG, and transport favours FDG over glucose. Although there are several different estimates on the normal value of LC in the brain, the estimates are always less than 1.0, representing that in normal condition the phosphorylation is the rate-limiting step in glucose uptake. In supply limited conditions (hypoglycemia and ischemia) LC increases as shown by Crane et al. (1981) and Hawkins et al. (1981).
Lumped constant is a function of the rate constants (Sokoloff et al. 1977).
The variability of LC results primarily from changes in
k3/k2 for glucose and for FDG (k3*/k2*)
as is expressed in below (Phelps et al. 1983):
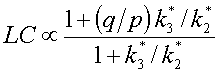
Phelps et al. (1983) used values p=0.50 and q=1.67 (q/p=3.34) to estimate the changes in LC between normal and ischemic brain regions. This equation was used by Sasaki et al. (1986) to estimate whether LC is uniform over the whole brain.
Kuwabara and Gjedde (1990; 1991) derived equation for LC which is independent
of the model used:
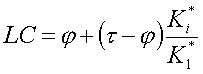
, where Ki* is the unidirectional clearance from
the circulation to the metabolic compartment
(Ki*=K1*k3*/(k2*+k3*)),
τ is the ratio between FDG and glucose clearances
(K1*/K1), and φ is the phosphorylation ratio
between FDG and glucose (k3*/k3).
Kuwabara and Gjedde (1991) used estimates τ=1.10 and φ=0.30.
Before that, Crane et al. (1983) have used estimates 1.67 and 0.55,
respectively, in rat studies.
Recommended values for using as LC
The recommended LC for brain [18F]FDG studies is 0.65, if irreversible uptake is assumed (3-parameter model or Gjedde-Patlak plot without kLOSS), and LC=0.81, if dephosphorylation is considered (4-parameter model or Gjedde-Patlak plot with kLOSS) (Wu et al. 2003).
In rat brain studies, lumped constant of 0.71 is recommended (Tokugawa et al., 2007; Krohn et al., 2007).
Estimation of metabolic rate of glucose
Use always Gjedde-Patlak graphical analysis for calculation of metabolic rate of glucose:
Estimation of parameters of compartmental model for brain
PET data
ROIs can be drawn and calculated from dynamic images as usual.
If old regional data is in *.roi.kbq file, it must be converted to
DFT format using
nci2dft, e.g.
nci2dft ua2826dy1.roi.kbq ua2826dy1.dft
Plasma data
Usually, manual samples are collected for the measurement of concentration of FDG in plasma. Blood samples are processed in the PET blood laboratory to time-activity curves, which can be used as such.
For better understanding, see also the documentation on blood data processing.
Correction for time delay
For Gjedde-Patlak analysis, correction for time delay is not required, but the estimates of compartmental model parameters may be very sensitive to the effect of time delay.
Estimation of K1, k2, k3 and k4 for FDG
Compartment model fit for the brain can be calculated using
fcmrglu,
e.g.:
fcmrglu ua2826ap.delay.kbq ua2826dy1.dft 5.2 ua2826fcmrglu.res
This programs writes the results in an ASCII text file (*.res); more
information on result files.
This program can also be used to estimate the LC at different study conditions; in that case, make sure that you are using appropriate values for τ and φ. Note that the brain model must not be applied to skeletal muscle!
Myocardium
Please read MET5731. Recommended LC for Patlak analysis of heart FDG studies is 1.
Skeletal muscle
Please read MET5736 and Bertoldo et al., 2001. Recommended LC for Patlak analysis of skeletal muscle FDG studies is 1.2 (Peltoniemi et al., 2000).
Lungs
Lung-specific model may be required (Schroeder et al., 2008).
